Question

A1=9, a3=17, find S5

Answer 1

`S_n=n((a_1+a_n)/(2))`

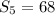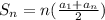
To find S5 first you need to find a5 (fith term)

Use the given data in the arithmetic sequence formula to find the common difference:

`\begin{gathered} a_n=a_1+(n-1)d \\ \\ a_1=9 \\ a_3=17 \\ n=3 \\ \\ 17=9+(3-1)d \\ 17=9+2d \\ 17-9=2d \\ 8=2d \\ (8)/(2)=d \\ \\ d=4 \end{gathered}`

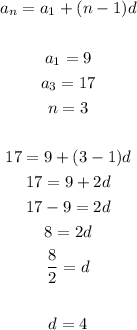
Use the common difference (a1) and the first term (a1) to write the formula of the given sequence:

`a_n=9+(n-1)4`

Find the 5th term:

`\begin{gathered} a_5=9+(5-1)4 \\ a_5=9+4\cdot4 \\ a_5=9+16 \\ a_5=25 \end{gathered}`

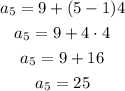
Use the formula of Sn (written in the first line in the page) to dinf S5:

`\begin{gathered} S_5=5((9+25)/(2)) \\ \\ S_5=4((34)/(2)) \\ \\ S_5=(136)/(2) \\ \\ S_5=68 \end{gathered}`

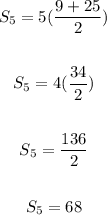
Then, S5 is 68

`S_5=68`