SOLUTION to question 8.
The area of the shaded portion is caculated by using the formula
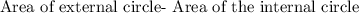
Hence
Area of the bigger circle will be obtain using the formula
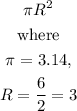
substitute into the formula, we have
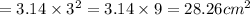
Hence
Area of the bigger circle is 28.26cm²
There area of the bigger circle will be
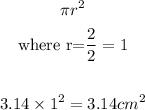
Hence
The ares of the internal circle is 3.14cm²
Hence
There area of the shaded portion is
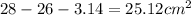
Therefore
The area of the of the shaded portion is 25.12cm²