Question

CD is the diameter of a circle whose center is the point (2,1). If the coordinates of C are (0,-2). find the coordinates of D.

Answer 1

D = (4, 4)

Step-by-step explanation:

The center of the circle is the midpoint of the segment CD. So, if C has coordinates (x1, y1) and D has coordinates (x2, y2), the coordinates of the center are (x, y) and are calculated as:

`\begin{gathered} x=(x_1+x_2)/(2) \\ y=(y_1+y_2)/(2) \end{gathered}`

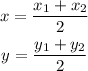
Then, we can replace (x, y) by (2, 1) and (x1, y1) by (0, -2) and solve for x2 and y2 as:

`\begin{gathered} 2=(0+x_2)/(2) \\ 2\cdot2=(0+x_2)/(2)\cdot2 \\ 4=0+x_2 \\ 4=x_2 \end{gathered}`
`\begin{gathered} 1=(-2+y_2)/(2) \\ 1\cdot2=(-2+y_2)/(2)\cdot2 \\ 2=-2+y_2 \\ 2+2=-2+y_2+2 \\ 4=y_2 \end{gathered}`

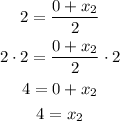
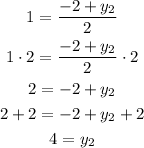
So, the coordinates of D(x2, y2) are (4, 4)