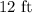Answer:
The length of AB is;
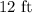
Step-by-step explanation:
Given the isosceles trapezoid in the attached image.
The length of line segment AE will be;
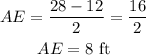
We can then use the Pythagorean theorem to solve for the length of the line segment AB;
![\begin{gathered} AB^2=AE^2+BE^2 \\ AB^2=8^2+9^2 \\ AB^2=64+81 \\ AB=\sqrt[]{64+81} \\ AB=\sqrt[]{145} \\ AB=12.04ft \\ AB=12\text{ ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3kq20zdvth3egleadn3s5yh00cs72so72y.png)
Therefore, the length of AB is;