Question

T- shirts at a flea market cost $4.50 each and shorts costs $6 each. you have $108A. write an equation that models the possible combinations of t-shirts (t) and shorts (s) you can buyB. if you purchase 6 shorts, how many t-shirts can you buy? show your work. write your answer in a complete sentence.C. if you purchase 10 shirt's z what is the maximum number or shorts you can buy? include evidence to support your answer. write your answer in a complete sentence

Answer 1

A.

Let t be the number of t-shirts you buy and s the number of shorts you buy.

Since each t-shirt you buy cost $4.50 the total cost for t-shirts is:

`4.5t`

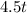
Since each short you buy cost $6 the total cost for shorts is:

`6s`

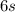
The total cost of your purchase is:

`4.5t+6s`

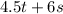
Since you have a total of $108 the equation that models the possible combinations of your purchase is:

`4.5t+6s=108`

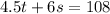
B.

If you buy 6 shorts that means that s=6, plugging this value into the equation above and solving for t we have:

`\begin{gathered} 4.5t+6(6)=108 \\ 4.5t+36=108 \\ 4.5t=108-36 \\ 4.5t=72 \\ t=(72)/(4.5) \\ t=16 \end{gathered}`

Therefore, If you purchased 6 shorts then you can buy 16 t-shirts.

C.

If you buy 10 shirts that means that t=10, plugging this value into the equation in part A and solving for s we have:

`\begin{gathered} 4.5(10)+6s=108 \\ 45+6s=108 \\ 6s=108-45 \\ 6s=63 \\ s=(63)/(6) \\ s=10.5 \end{gathered}`

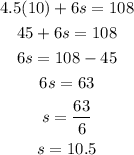
Now, since you can't buy half of a short the answer above means ( that:

If you buy 10 shirts then you can buy a maximum of 10 shorts, this wil be a total of $103