For this problem, we are given the image of a quadrilateral, with the measurements for length and width. We need to use this information to determine how long the diagonal would have to be for this image to be a rectangle.
In order to solve this problem, it is helpful to make a sketch of the situation, as shown below:
As shown in the image below, we can create a right triangle with the diagonal of the rectangle. Due to this, we can apply Pythagora's theorem to determine the length of the diagonal.
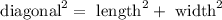
Applying the provided data, we have:
![\begin{gathered} d^2=7.5^2+15^2 \\ d^2=56.25+225 \\ d^2=281.25 \\ d=\sqrt[]{281.25} \\ d=16.8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f25a3b8zsq0a5rj78zufi5utley1oj3hcg.png)
For the tabletop to be a perfect rectangle, the diagonal would have to be approximately 16.8 inches long.