To find the sum of the first n terms of an arithmetic sequence, we use the formula (which you also gave):
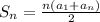
Let's find a1 first by substituting 1 for i.
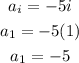
Next, let's solve for the last term, a30.
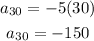
Let's use these values to solve for the sum.
![\begin{gathered} S_(30)=(30[-5+(-150)])/(2) \\ \\ S_(30)=(30(-155))/(2) \\ \\ S_(30)=15(-155) \\ \\ S_(30)=-2,325 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r2pai3i6xdznjwa9joft7ru4618prxro08.png)
The answer is -2,325.