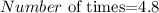
Step-by-step explanation
Step 1
find the volume of the cone:
The formula for the volume of a cone is
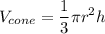
where
then , to find the volume of cone"1
let
r= 6 in
h=5 in
Now, replace
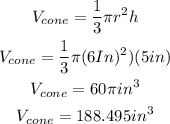
Step 2
Now, the volume of a sphere:
The formula for the volume of a sphere is
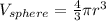
then,let
radius= 6 inches
Now, replace.
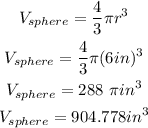
Step 3
finally, to know how many times the volume of the sphere is greater than the volume of the cone , do a division

so, the answer is 4.8
I hope this helps you