Answer:
Explanation:
Here is what we know;
Both Kathy and Cheryl cover the same distance ( one course).
Kathy completes the course in 3.6 hours.
Kathy's speed is 2 miles/hour faster than Cheryl's
Cheryl completes the course in 6 hours
Cheryl's speed is yet unkown.
Now, the speed v is defined as
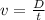
where D is the distance covered and t is the time taken.
Now, let us say D = distance of one course. Then in Kathy's case, we have
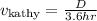
since Kathy's speed is 2 miles per hour faster than Cheryl's, we have
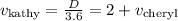
For Cheryl, we know that
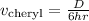
or simply
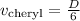
Putting this into the equation for Kathy's speed gives
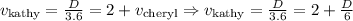
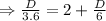
We have to solve for D, the distance of a course.
Subtracting D/6 from both sides gives
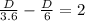
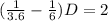
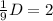
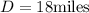
Hence, the distance of a course is 18 miles.
With the value of D in hand, we can now find the velocity of Kathy and Cheryl.
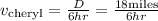
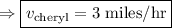
Hence, Cheryl's speed is 3 miles/hr.
Next, we find Kathy's speed.
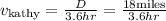
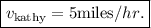
Hence, Kathy's speed is 5 miles/hr.
Therefore, to summerise,
Kathy's speed = 5 miles/hr
Cheryl's speed = 3 miles/hr