The formula is
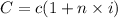
Where C is the total, c initial capital, n the number of years and i interest percentage
We can modify the formula to express the total won
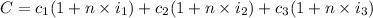
Where c1 is the par 5%, C2 the par at 11% and c3 the par at 14%
i1,i2 and i3 the percentage of interest applied to each part
as a total you must use the total earned plus the initial capital
so replacing
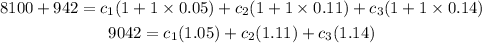
this was our first equation
the next comes from: the sum of all inverted parts is 8100
so
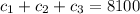
hitrd equation is from: The amount of money invested at 14% was $500 more than the amounts invested at 5% and 11% combined.
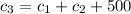
Solution of the equations
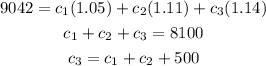
we replace the third equation on the second
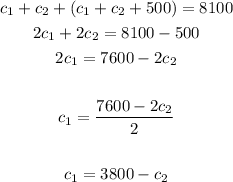
now replace c3 and c1 on the first equation to find c2
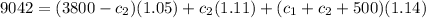
now replace c1 again
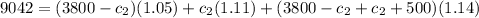
and find c2
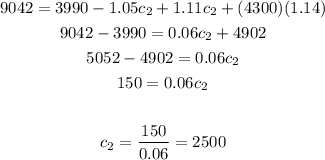
the value of c2 or the part at 11% is $2,500
now we can replace c2 in one of the equations we solved, for example this
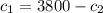
and find c1
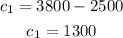
the value of c1 or the part at 5% is $1,300
now we can repalce c1 and c2 on the equation
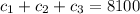
and find c3
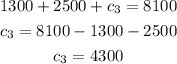
the value of c3 or the part at 14% is $4,300
the total values are
part at 11% is $2,500
part at 5% is $1,300
part at 14% is $4,300