Solution
How fast is the distance from the observer to the balloon:
Initial distance between observer and balloon is d = 150 ft;
the speed of the balloon is v = 8 ft/sec;
when balloon is h =50 ft high, final distance can be calculated as;
![\begin{gathered} d^2_f=h^2+d^2_0 \\ d_f=\sqrt[]{h^2+d^2_0} \\ d_f=\sqrt[]{150^2+50^2} \\ d_f=\sqrt[]{25000} \\ d_f=158.114ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bcula9anou4ixdnem4vj4pp316tm0d7w2z.png)
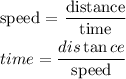
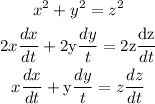
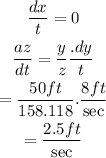
Therefore the distance from the observer increasing = 2.5ft/sec