we have the formula
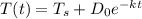
step 1
Find out the value of k
we have
T=150 degrees
Ts=70
To=200
Do=200-70=130
t=10 min
substitute
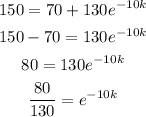
Apply ln on both sides
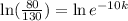
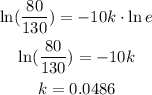
substitute the value of k in the given formula
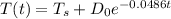
Now
For t=20 min
Ts=70
To=200
Do=200-70=130
substitute
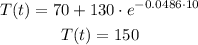
The answer is option A