We must compute the derivative of the function at x = 2:

using the limit definition.
1) We write explicitly the derivative as a limit:
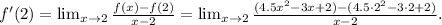
2) We simplify the expression above:
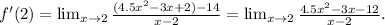
If we replace x by 2, we get a 0 in the numerator and denominator. So this is a limit of the type 0/0 where we can apply L'Hopital's rule.
3) We apply L'Hopital's rule, which consists of taking the derivative of numerator and denominator, we get:

4) Now, we see that there is no problem to replace x by 2, doing that we get:
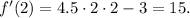
Answer: f'(2) = 15