Question

Find the 32th term of a arithmetic sequence with a1=4 and d =3.

Answer 1

The nth term of a arithmetic sequence can be found with the expression below:

`a_n=a_1+(n-1)\cdot d`

Where "an" is the nth term, "a1" is the first term, "n" is the position of the nth term and d is the ratio of the squence. Applying the data from this problem we can make n=32, a1 = 4 and d= 3 to solve for an. We have:

`\begin{gathered} a_(32)=4+(32-1)\cdot3 \\ a_(32)=4+(31)\cdot3 \\ a_(32)=4+93 \\ a_(32)=97 \end{gathered}`

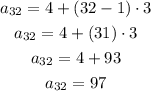
The 32th term of this sequence is 97.