Question

Solve the equation for x, accurate to three decimal places: e^{4x} − 6e^{2x} = 16.x = 1.040x = 1.039x = 1.386x = 0.347

Answer 1

Hello!

We have the following equation:

`e^(4x)−6e^(2x)=16`

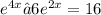
First, we can rewrite this expression to obtain the same base in both variables, look:

`(e^(2x))^2−6(e^(2x))=16`
`(e^(2x))^2−6(e^(2x))=16`
`(e^(2x))^2−6(e^(2x))=16`

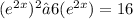
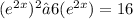
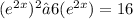
To make it easier, we can replace where's e^{2x} with any letter. I'll replace it with s, look:

`\begin{gathered} (e^(2x))^2-6(e^(2x))=16 \\ \\ \left(e^(2x)\right)=s \\ \\ s^2−6s=16 \end{gathered}`

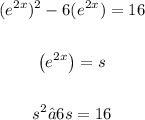
Now, let's solve this quadratic equation:

`\begin{gathered} s^2-6s=16 \\ s^2-6s-16=0 \end{gathered}`
`\begin{gathered} s=(-b\pm√(b^2-4ac))/(2a)=(-(-6)\pm√((-6)^2-4*1*(-16)))/(2*1) \\ \\ =(6\pm√(36^+64))/(2*1)=(6\pm√(100))/(2)=(6\pm10)/(2) \\ \\ s^(\prime)=(6+10)/(2)=(16)/(2)=8 \\ \\ s^(\prime)^(\prime)^=(6-10)/(2)=-(4)/(2)=-2 \end{gathered}`

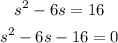
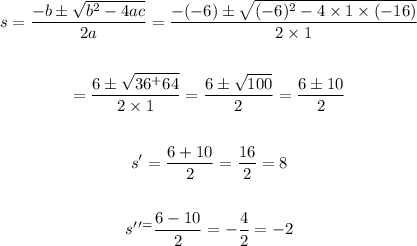
At this moment, we obtained two possible values for this equation: -2 and 8.

Now, let's cancel the replacement that we did before. s will turn back to be e^{2x}.

`\begin{gathered} e^(2x)=-2\\otin\mathrm{R} \\ e^(2x)=8\text{ }\in R \\ \end{gathered}`

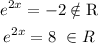
So, let's solve the second line:

`\begin{gathered} e^(2x)=8 \\ \ln(e^(2x))=\ln(8) \\ 2x=\ln(2^3) \\ 2x=3\ln(2) \\ x=(3\ln(2))/(2) \end{gathered}`

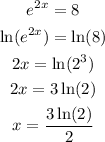
Using a calculator, we will obtain x = 1.03972.

As we have to round to three decimal places, the answer will be x = 1.040.