Question

Write an equation in standard form of the parabola that has the same shape as the graph of f(x) = 5x^2, but which has a minimum of 9 at x = 5.

Answer 1

The graph f(x)=5x^2 is a parabola that opens upwards and which minimum point is at x=0. We need that, once f(x) is transformed, g(5)=9.

For that, we need to translate the graph on the plane. First, 9 units up and then 5 units to the right; this is:

`translatedf(x)\to_{}g(x)=5(x-5)^2+9`

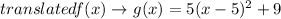
Now, we need to write g(x) into standard form. In general, the standard form of a quadratic equation is

`f\mleft(x\mright)=a\mleft(x-h\mright)^2+k`

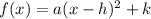
Where (h,k) is the vertex of the parabola.

Therefore, g(x) is already written in the standard form, a=5 and (h,k)=(5,9).

The answer is 5(x-5)^2+9