From the information provided by the statement, you know that
*Ann draws 2/16 of the playground
*Susan draws 6/16 of the playground because she draws 3 times as much as Ann so
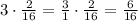
*Louise draws 3/16 because she draws half as much as Susan, so
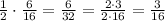
*Sam draws 2/16 because she draws 1 less section than Louise
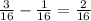
Now, let x be the fraction of the playground that still needs to be drawn. Then, you have

Therefore, 3/16 of the playground still needs to be drawn.