Question

What is the total cost of joining the club and playing 10 games during the year

Answer 1

To answer this question, first, at all, we need to find the equation for the line in the graph. For this, we need to take two points from the graph, and then calculate the slope of the line, and then we can obtain the equation of the line taking one of the points in the point-slope form of the linear equation. Then, we have:

1. Slope of the line

We can get the points: (0, 90) and (1, 120).

Then, we have that:

x1 = 0,

y1 = 90,

x2 = 1,

y2 = 120

Then, the slope is:

`m=(y_2-y_1)/(x_2-x_1)\Rightarrow m=(120-90)/(1-0)\Rightarrow m=30`

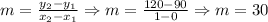
Therefore, the slope m = 30. We can use any point of the line to find this slope.

2. Apply the point-slope form of the line equation:

We can use the point (1, 120)

x1 = 1

y1 = 120

`y-y_1=m(x-x_1)\Rightarrow y-120=30(x-1)\Rightarrow y-120=30x-30`

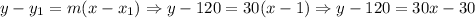
Then, we have:

`y=30x-30+120\Rightarrow y=30x+90`

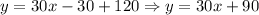
Now, we have the line equation.

We need to substitute the value of 10 in the independent variable x.

`y=30\cdot(10)+90\Rightarrow y=300+90\Rightarrow y=390`

Then, the total cost of joining the club and playing 10 games during the year is $390. We can see that this cost is represented by a line and this line is y = 30x + 90.

We can check our result if we substitute the values of x in the graph into the line equation. For example, if we have x = 3, and x = 5, we have:

`f(3)=y=30\cdot(3)+90=90+90=180,(3,180)`

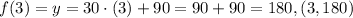
And

f(5) = 240 (5, 240), as the coordinates in the graph (which tells us that our equation line is correct.)