Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. Students in Mrs. McGee's third grade class are working on times tables, and they demonstrate mastery by passing tests. Rebecca has passed 12 tests so far. Her classmate, Marie, has passed 3 tests of them. From now on, Rebecca plans to take and pass 2 tests per week. Meanwhile, Marie plans to do 5 per week. At some point, Rebecca will catch up to Marie. How long will it take? How many tests will each child have passed? In weeks, the children will each have passed tests.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Represent the unknown terms

Let x represents the number of weeks

Let y represents the total number of test passed

STEP 2: Interpret the statements

For Rebecca

`y=2x+12`

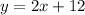
For Marie

`y=5x+3`

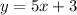
STEP 2: Find the number of weeks they will pass the same amount of test.

This means that y will be equal to y

`\begin{gathered} y=y \\ 2x+12=5x+3 \\ 2x-5x=3-12 \\ -3x=-9 \\ x=(-9)/(-3)=3\text{ weeks} \end{gathered}`

Hence, they will both pass the same number of tests in 3 weeks

STEP 3: Find the amount of tests passed

For Rebecca

`\begin{gathered} 2x+12 \\ x=3 \\ y=2(3)+12=6+12=18 \end{gathered}`

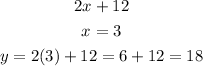
For Marie

`\begin{gathered} y=5x+3 \\ x=3 \\ y=5(3)+3=15+3=18 \end{gathered}`

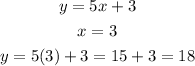
Both will pass 18 tests in 3 weeks

ANSWER:

In 3 weeks, the children will each have passed 18 tests.​