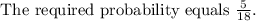Question

Two dice are rolled what is the probability that the sum of the numbers rolled is either 6 or 8 express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth

Answer 1

Given:

Two dice are rolled.

Required:

What is the probability that the sum of the numbers rolled is either 6 or 8?

Step-by-step explanation:

The probability,

`Probability(P)=\frac{\text{ Numebr of favorable outcomes}}{\text{ Total number of outcomes}}`

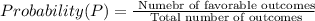
There are 36 possible results when two dice are rolled.

The results add to 6 are 1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1.

The results add to 8 are 2 + 6, 3 + 5, 4 + 4, 5 + 3, 6 + 2.

5 rolls of two dice add to 6 and 5 rolls add to 8.

So,

`\begin{gathered} P=(10)/(36) \\ P=(5)/(18) \end{gathered}`

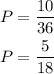
Answer:

`\text{ The required probability equals }(5)/(18).`