Step-by-step explanation
Given the equations;
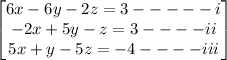
We are asked to find its solution.
First, we isolate x from the first equation
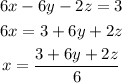
Substitute x in the remaining equations
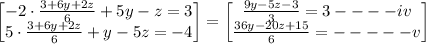
From equation iv above, we will isolate y
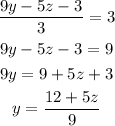
Substitute y in equation v
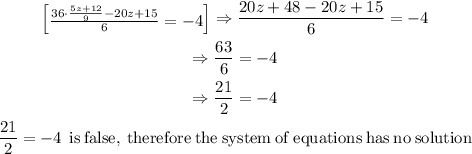
Answer: No solution