We can do the following steps to solve the exercise:
Step 1: We find the volume of the tank. For this, we use the formula to calculate the volume of a hemisphere.
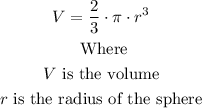
Then, we have:
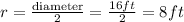
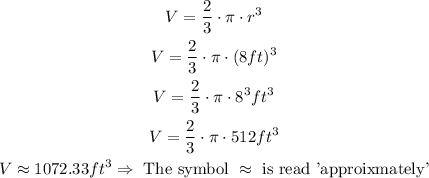
Step 2: We apply the density formula to find the total weight of the liquid in the tank.
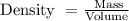
We replace the know values into the above formula.

Therefore, the total weight of the liquid in the tank rounded to the nearest full pound is 99,727 pounds.