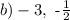
Step-by-step explanation
The zero of a function is any replacement for the variable that will produce an answer of zero,so to find the zeros of this function we need set the equation = 0, and then solve for x
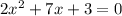
The rigth side of the equation is zero, so we can solve
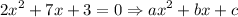
we can use the quadratic formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replace} \\ x=\frac{-7\pm\sqrt[]{7^2-4\cdot2\cdot3}}{2\cdot2} \\ x=\frac{-7\pm\sqrt[]{49-24}}{4} \\ x=\frac{-7\pm\sqrt[]{25}}{4} \\ x=(-7\pm5)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ydmnmhlypzz6kr4ser1vyofrhnmwnrvonb.png)
therefore.
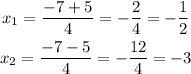
so, the answer is
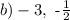
I hope this helps you