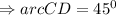Answer:
From the image in the question, we have that
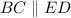
Given also
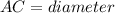
From the given information above, we will have that
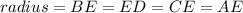
From the triangle BCE,
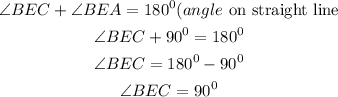
Since the triangle BEC is bounded by two radii CE and BE,
Then we can say that the triangle BEC is an Isosceles triangle
A triangle with two sides of equal length is an isosceles triangle. The two equal sides of an isosceles triangle are known as 'legs' whereas the third or unequal side is known as the 'base'. Many things in the world have the shape of an isosceles triangle.
Two angles are also equal and they are given below as
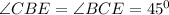
Since,
BC is parallel to ED, we will have the final answer as
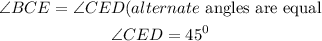
Therefore,
The final answer for arc CD is