Question

Rachel bought a desktop computer and a laptop computer. Before finance charges, the laptop cost $300 more than the desktop. She paid for the computersusing two different financing plans. For the desktop the interest rate was 9% per year, and for the laptop it was 7% per year. The total finance charges for oneyear were $365. How much did each computer cost before finance charges?

Answer 1

We are asked to determine the cost of a desktop computer and a laptop computer.

Let "x" be the cost of the desktop computer and "y" be the cost of the laptop computer.

We are given that the laptop costs $300 more than the desktop, therefore, we have:

`y=x+300,(1)`

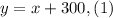
Now, we are also given that the total interest paid for both computers is $365.

We have:

`i_d+i_l=365`

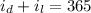
Where:

`\begin{gathered} i_d=\text{ interest paid for desktop} \\ i_l=\text{ interest paid for laptop} \end{gathered}`

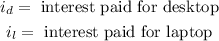
Now, since the interest paid for the desktop is 9%, we have that it must be equal to:

`i_d=0.09x`

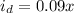
The interest paid for the laptop is 7%, therefore, it must be:

`i_l=0.07y`

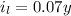
Now, we substitute in the equation for the total interest paid:

`0.09x+0.07y=365,(2)`

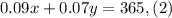
We get two equations and two variables. To solve the system we will substitute the value of "y" from equation (1) into equation (2):

`0.09x+0.07(x+300)=365`

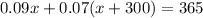
Now, we apply the distributive law on the parenthesis:

`0.09x+0.07x+21=365`

Now we add like terms:

`0.16x+21=365`

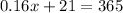
Now, we solve for "x", first by subtracting 21 from both sides:

`\begin{gathered} 0.16x=365-21 \\ 0.16x=344 \end{gathered}`

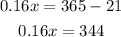
Now, we divide both sides by 0.16:

`x=(344)/(0.16)`

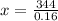
Solving the operations:

`x=2150`

Now, we plug in the value of "x" in equation (1):

`\begin{gathered} y=2150+300 \\ y=2450 \end{gathered}`

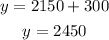
Therefore, the cost of the desktop is $2150 and the cost of the laptop is $2450.