The function is given as,
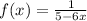
Differentiating both sides with respect to 'x',
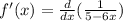
According to the reciprocal rule,
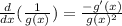
Comparing with the expression,
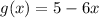
The corresponding derivative is given by,
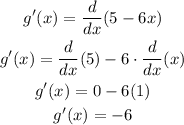
Substitute the values in the formula,
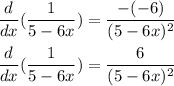
So the derivative of the given function becomes,

Thus, the derivative of the given function is obtained as,
