Question

Let point B represent the intersection point of the height, DB, and the base CE. Determine the coordinates of point B.

Answer 1

Given

Let point B represent the intersection point of the height, DB, and the base CE.

To determine the coordinates of point B.

Step-by-step explanation:

It is given that,

Let point B represent the intersection point of the height, DB, and the base CE.

That implies,

Then,

The equation of the line CE is,

`\begin{gathered} (y_-y_1)/(y_2-y_1)=(x-x_1)/(x_2-x_1) \\ (y-1)/(-5-1)=(x-1)/(-2-1) \\ (y-1)/(-6)=(x-1)/(-3) \\ (y-1)/(2)=x-1 \\ y-1=2(x-1) \\ 2x-2=y-1 \\ 2x-y-2+1=0 \\ 2x-y-1=0\text{ \_\_\_\_\_\lparen1\rparen} \end{gathered}`

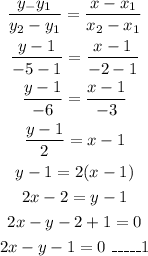
Since DB is height(altitude) of the triangle DCE.

Then, the line DB is perpendicular to the line CE.

That implies, the equation of the line DB perpendicular to the line CE (1) is,

`x+2y+k=0\text{ \_\_\_\_\_\lparen2\rparen}`

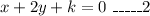
Since it passes through the point D(7,1).

Then,

`\begin{gathered} 7+2+k=0 \\ 9+k=0 \\ k=-9 \end{gathered}`

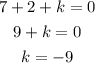
Hence, the equation of the line DB is

`x+2y-9=0\text{ \_\_\_\_\_\lparen3\rparen}`

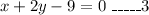
Also, since B is the point of intersection to the lines DB and CE,

Then, the point of intersection B is obtained by solving (1) and (3).

That is,

`\begin{gathered} (1)*2\Rightarrow4x-2y-2=0 \\ (2)*1\Rightarrow x+2y-9=0 \\ Adding\Rightarrow5x-11=0 \\ \Rightarrow5x=11 \\ \Rightarrow x=(11)/(5) \end{gathered}`

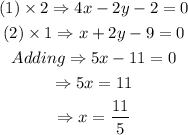
Substitute x in (1)

Then,

`\begin{gathered} 2((11)/(5))-y-1=0 \\ (22)/(5)-y-1=0 \\ y=(22)/(5)-1 \\ y=(22-5)/(5) \\ y=(17)/(5) \end{gathered}`

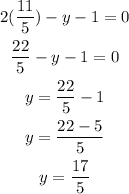
Hence, the point of intersection is B(11/5, 17/5).