Question

at noodles and company restaurant, the probability that a customer will order a nonalcoholic beverage is .33. find the probability that in a sample of 8 customers, none of 8 will order a nonalcoholic beverage?

Answer 1

This is a binomial probability problem. The probability of "x" is given by the formula:

`P(x)=(n!)/((n-x)!x!)p^xq^(n-x)`

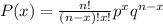
Where

n is the total number in sample

x is the event

p is the probability of success

q is " p - 1 ", or probability of failure

Given,

n = 8

p = 0.33

q = 1 - 0.33 = 0.67

x = none, so, x = 0

Substituting into the formula, we have:

`\begin{gathered} P(x)=(n!)/((n-x)!x!)p^xq^(n-x) \\ P(x=0)=(8!)/((8-0)!0!)(0.33)^0(0.67)^(8-0) \\ P(x=0)=(8!)/(8!)(1)(0.67)^8 \\ P(x=0)=(1)(1)(0.67)^8 \\ P(x=0)=0.67^8 \\ =0.0406 \end{gathered}`

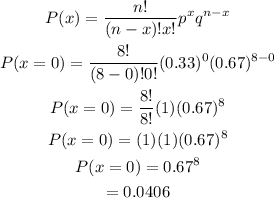
Answer

0.0406