ANSWER and EXPLANATION
PART A
The solution to the system of linear equations is (-4, 4)
PART B
The solution to any system of graphed equations is the point on the graph where the two lines intercept.
Therefore, since f(x) and g(x) intercept at (-4, 4), it is the solution to the system of linear equations.
PART C
To prove that the answer is correct, we can solve it with another method i.e. equate the two equations and find x. The value of both functions at that value of x will be the same.
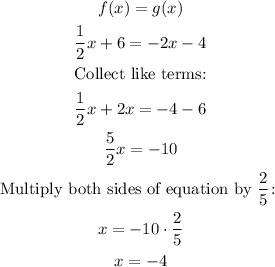
Find the corresponding values of f(x) and g(x):
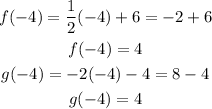
Therefore, we have proven that the answer is correct.