Question

Use the following probabilities to answer the question. It may be helpful to sketch a Venn diagram.P(A)=0.41P(B)=0.34 and P(AandB)=0.25 P(B∣notA)=

Answer 1

So to solve this question let's use the following table:

In this case

`\bar{A}`

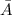
is not A

and

`A\cap B`

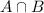
is AandB

So let's apply as the first step number 5 of the table

`P(B|\bar{A})=\frac{P(B\cap\bar{A})}{P(\bar{A})}`

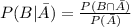
Now for the numerator let's apply 3 and for the denominator apply 1

And we replace the probabilities

`(0.34-0.25)/(1-0.41)=(0.09)/(0.59)=0.15`

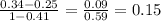
Answer: P(B∣notA)=0.15