Question

I need help with my homework I have to go to sleep so pls go fast

Answer 1

Find the slope of the data, using the formula of the slope:

`m=(y2-y1)/(x2-x1)`

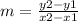
Use 2 pairs of data to find it:

`\begin{gathered} m=(107.50-58.50)/(4-2) \\ m=(49)/(2) \\ m=24.50 \end{gathered}`

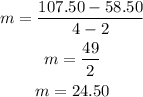
In this case the slope is 24.50.

It represents the cost per ticket.

Now, we can use this slope and a pair of data to find the equation that represents this situation, using the point slope formula:

`\begin{gathered} y-y1=m(x-x1) \\ y-58.50=24.50(x-2) \\ y-58.50=24.50x-49 \\ y=24.50x-49+58.50 \\ y=24.50x+9.50 \end{gathered}`

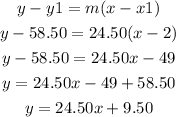
According to this the y intercept of the equation is 9.50, which is also the service charge.

Knowing this information allows us to determine that the statements that are true are I and II.