Question

Hello! I need some help with this homework question, please? The question is posted in the image below. Sections a and b are already completed. Q10

Answer 1

`\begin{gathered} \text{Given} \\ f(x)=\sqrt[]{x} \\ g(x)=4x+7 \end{gathered}`

Part C: Solving for (f o f)(x)

`\begin{gathered} (f\circ f)(x)=f\Big(f(x)\Big) \\ (f\circ f)(x)=f\Big{(}\sqrt[]{x}\Big{)} \\ (f\circ f)(x)=\sqrt[]{(\sqrt[]{x})} \\ \\ \text{Therefore,} \\ (f\circ f)(x)=\sqrt[4]{x} \end{gathered}`

Since the resulting function is a radical function with a even degree (fourth root), we cannot have a negative fourth root, therefore, the domain of the function is

`\text{Domain: }\mleft\lbrace x|x\ge0\mright\rbrace`

Part D: Solving for (g o g)(x)

`\begin{gathered} (g\circ g)(x)=g\Big{(}g(x)\Big{)} \\ (g\circ g)(x)=g\Big{(}4x+7\Big{)} \\ (g\circ g)(x)=4(4x+7)+7 \\ (g\circ g)(x)=16x+28+7 \\ \\ \text{Therefore,} \\ (g\circ g)(x)=16x+35 \end{gathered}`

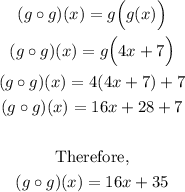
Since the resulting function composition is a polynomial (linear function), then the domain of the function is all real numbers.