Question

An auditorium has 57 rows of seats. The first row contains 60 seats. As you move to the rear of the auditorium, each row has 2 more seats than the previous row.How many seats are in the row 17 ? How many seats are in the auditorium

Answer 1

Step-by-step explanation

Assuming that y represents the number of seats in x rows, the following linear equation applies:

`N(seats)=Number\text{ of seats in first row+\lparen n-1\rparen rate of change}`

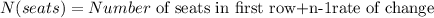
Where the rate of change = 2

This is an arithmetic series

As the first row has 60 seats, and the 17th row is 16 rows behind.

N(17)=60+(17-1)*2 = 92 seats

-Therefore, there are 92 seats in the row #17

-To get the number of seats in the auditorium, we need to consider that the last row is #57.

Plugging in the values into the equation:

`N(57)=60+(57-1)*2`

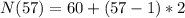
Multiplying numbers:

`N(57)=172`

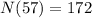
Applying the Sum:

Sum=(1/2) {first row + last row}* n rows

The first row has 60 seats and the last one 172. Substituting terms:

`\sum_{1\mathop{=}1}^(57)(1)/(2)(first\text{ row+last row})*n\text{ rows=}(1)/(2)(60+172)*57=6612\text{ seats}`

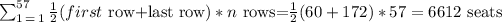
In conclusion, there are 6612 seats in the auditorium.