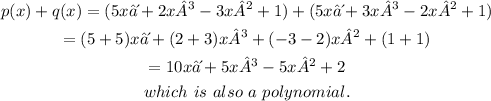Given
The polynomials,
a. 2x³ +-3x² +1 +5x⁴
b. 5x⁴ + 2x³-3x² + 1
c.-3x² +1+5x⁴+ 2x³
d. 1-3x²+2x³ + 5x⁴
To find:
A) Which polynomial is a fourth-degree polynomial in standard form? Explain how you know it is a fourth-degree polynomial and how do you know it's in standard form.
B) Explain the closure property as it relates to polynomials and give an example.
Step-by-step explanation:
It is given that,
The polynomials,
a. 2x³ +-3x² +1 +5x⁴
b. 5x⁴ + 2x³-3x² + 1
c.-3x² +1+5x⁴+ 2x³
d. 1-3x²+2x³ + 5x⁴
Part A)
From, the above polynomials,
b. 5x⁴ + 2x³-3x² + 1 is the fourth degree polynomial in its standard form.
Reason:
Because the standard form of a polynomial starts with its highest degree and ends with lowest degree in a descending order.
Part B)
Also,
Closure property of a polynomial states that,
The addition or subtraction of two polynomials is again a polynomial.
For example,
Consider two polynomials,
p(x) = 5x⁴ + 2x³-3x² + 1, and q(x) = 5x⁴ + 3x³-2x² + 1
That implies,