aAs given by the question
There are given that the vertices and asymptote:
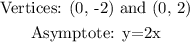
Now,
First find the center (h, k):
So,
The center is the midpoint point of the vertices:
Then,
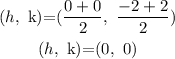
Now,
Find the value of a
So,
a is the distance of center to vertices
So,
![\begin{gathered} a=\sqrt[]{(0+2)^2+(0-0)^2} \\ a=\sqrt[]{4} \\ a=2 \\ a^2=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9brz30dx4btvdwtirm2wsq3jzcxd8x1phy.png)
Now,
From from the slope:
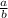
Then,
From the given asymptote, the slope of the equation is 2 which is given in the equation of asymptote.
So,
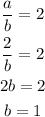
Now,
From the standard form of the hyperbola:

Then,
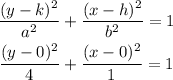
Hence, the equation of hyperbola is shown below:
