When we are performing a test of hypothesis, one of the steps is to calculate the test statistic.
This measure will allows us to evaluate the significance of the sample results.
In this case, the test statistic in a hypothesis test on a proportion can be written as:
![z=\frac{p-\pi}{\sqrt[]{(\pi(1-\pi))/(n)}}](https://img.qammunity.org/2023/formulas/mathematics/college/s1b46yjle5wtlys38j6vigm3u8ipxgk94s.png)
where
p: sample proportion
pi: population proportion, as expressed in the null hypothesis
n: sample size
"A research study claims that 68% of adults drink regularly Edwards conduct a random sample of 200 people and finds that 140 people drink regularly"
Then, in this case we are trying to prove that the proportion of a population differs from 0.68, we would write a null hypothesis that is:
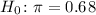
The sample size is n=200 gives and the sample proportion is p=140/200=0.70, we can calculate the test statistic as:
![\begin{gathered} z=\frac{p-\pi}{\sqrt[]{(\pi(1-\pi))/(n)}} \\ z=\frac{0.70-0.68}{\sqrt[]{(0.68\cdot0.32)/(200)}}=\frac{0.02}{\sqrt[]{0.001}}\approx(0.02)/(0.033)\approx0.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/eg82k94w3fotf1pwcl7n9v5dfjdd8isjmi.png)
This test statistic, z=0.6, will be use to evaluate the significance of this sample result.
Answer: the test statistic for this hypothesis test is z=0.6.