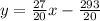The line passes through the point:
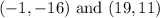
We can use the slope-intercept form of a linear equation to get the line:

where

The points are:
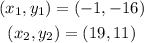
Using the formula, we have:
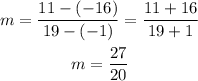
Thus, the equation is in the form:
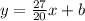
At the point (-1, -16), we have:
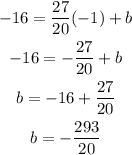
Therefore, the equation will be: