Question

Given the inequality 6x - 10y ≥ 9, select all possible solutionsD. (4, -2)E. (2, 8)F. (5, 2)

Answer 1

We have the inequality 6x-10y>=9 and we have to find if the points listed are possible solutions.

The inequality divides the plane in two halfs: the half on the line or above the line is part of the solution region. If the point lies in that region, is a solution to the inequality.

We can prove this without graphing the line by replacing the values in the inequality and veryfying that the inequality gives a true value.

D) Point (x,y) = (4,-2)

We replace x and y with the values of the point and solve:

`\begin{gathered} 6x-10y\ge9 \\ 6\cdot4-10(-2)\ge9 \\ 24+20\ge9 \\ 44\ge9\longrightarrow\text{True: (4,-2) is a solution} \end{gathered}`

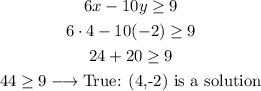
E) Point (2,8)

`\begin{gathered} 6\cdot2-10\cdot8\ge9 \\ 12-80\ge9 \\ -68\ge9\longrightarrow\text{False: (2,8) is not a solution} \end{gathered}`

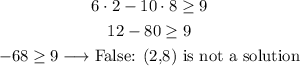
F) Point (5,2)

`\begin{gathered} 6\cdot5-10\cdot2\ge9 \\ 30-20\ge9 \\ 10\ge9\longrightarrow\text{True: (5,2) is a solution} \end{gathered}`

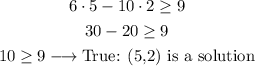
We now can graph the inequality and the points in order to check:

NOTE: (5,2) is close to the limit of the inequality, but it is in the solution region.