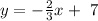Question

Give the equation of a line goes through the point (6,3) and is perpendicular to the line 3x-2y=4. Give your answer in slope intercept form

Answer 1

First let's find the slope of the line; 3x - 2y = 4

To do that , re-write the equation to be in the form y = mx + b

3x - 2y = 4

2y =3x - 4

Divide through the equation by 2

`y=(3)/(2)x\text{ -}(4)/(2)`
`y=(3)/(2)x-2`

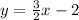
Comparing with y = mx + b

m = 3/2

Slope of perpendicula equation is given by

`m_1m_2=-1`

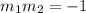
To find the slope of the new equation, substitute m1 = 3/2 and then solve for m2

`(3)/(2)m_2=\text{ -1}`

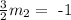
Multiply both-side by 2/3

`m_2=-(2)/(3)`

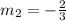
We now have the slope of the new equation

Let's go ahead to find the intercept of the new equation

Simply substitute x₁=6 y₁=3 m = -2/3 and then solve for intercept b in

y=mx + b

3 = (-2/3) (6) + b

3 = -4 + b

Add 4 to both-side

3 + 4 = b

7 = b

b = 7

To form the new equation, simply substitute m =-2/3 and b = 7 into y=mx + b

The new equation is;

`y=-(2)/(3)x+\text{ 7}`