Question

I need help question

Answer 1

- The critical points of a graph are the points where the turning points of the graph are zero.

- The turning points are gotten by differentiating the function after which we can equate to zero.

- This is done below:

`f(x)=2x^3-30x^2+126x-10`

- The way to differentiate is given below:

`\begin{gathered} Given\text{ }f(x)=x^n \\ f^(\prime)(x)=nx^(n-1) \\ \\ \text{ Thus, to differentiate the function }ax^n+bx^(n-1)+cx^(n-2)+dx^(n-3)... \\ f^(\prime)(x)=nax^(n-1)+b(n-1)x^(n-2)+c(n-2)x^(n-3)+... \end{gathered}`

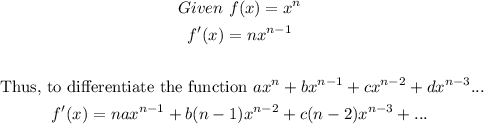
For example,

`\begin{gathered} f(x)=5x+6 \\ \text{ Differentiating, we have:} \\ f^(\prime)(x)=5(1)x^(1-1)=5 \\ \\ f(x)=10x^2+3x-20 \\ \text{ Differentiating, we have:} \\ f^(\prime)(x)=10(2)x^(2-1)+3(1)x^(1-1) \\ f^(\prime)(x)=20x+3 \end{gathered}`

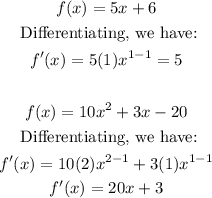
- The differentiation is done below:

`f^(\prime)(x)=6x^2-60x+126`

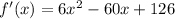
- The critical points are where f'(x)= 0. Thus, we have:

`\begin{gathered} 6x^2-60x+126=0 \\ 6x^2-42x-18x+126=0 \\ 6x(x-7)-18(x-7)=0 \\ (x-7)(6x-18)=0 \\ \\ x=7\text{ or }6x=18 \\ x=7\text{ or }x=3 \end{gathered}`

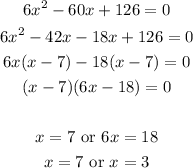
Final Answer

The critical points are x = 7 and x = 3