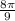SOLUTION:
Case: Arc length and Area of sectors
Given: The length of the arc and the angle subtended
Required: To find the area of the sector
Method:
Step 1: First we use the length of the arc to get the radius of the circle

Step 2: Use the radius to find the area of the sector
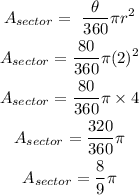
Final answer:
The Area of the sector in square units is