Question

Two of the math courses Business majors need to take are ElementaryStatistics and Business Calculus. In a random survey of 100 studentswho have declared as Business majors and are currently enrolled in atleast one of the two courses, 82 are enrolled in Elementary Statisticsand 57 are enrolled in Business Calculus. How many are currentlyenrolled in both courses? Hint: A Venn diagram can be helpful inorganizing the given information.

Answer 1

Step-by-step explanation

From statistics, we know the following relation:

`n(A\cap B)=n(A)+n(B)-n(A\cup B).`

Where:

• n(A) = # of elements in set A,

• n(B) = # of elements in set B,

,

• n(A U B) = # of elements in the union of sets A and B,

,

• n(A ∩ B) = # of elements in the intersection of sets A and B.

For this problem, we consider:

• n(A) = # of students enrolled in Elementary statistics = 82,

,

• n(B) = # of students enrolled in Business Calculus = 57,

,

• n(A U B) = total # of students = 100,

,

• n(A ∩ B) = # of students enrolled in both courses.

Replacing these data in the formula above, we get:

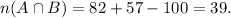
`n(A\cap B)=82+57-100=39.`Answer

There are 39 students enrolled in both courses.