We have that the arithmetic sequence is referred to a sequence that the difference between the numbers is constant. While the geometric sequence is a sequence where each number after the first is identified by multiplying the previous one by a fixed number.
a) Given:
57, 61, 65...
The difference is given by:
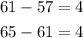
The difference between the numbers is 4, that is, a constant number. Therefore, It's an arithmetic sequence.
Answer: arithmetic sequence
b) The formula for the arithmetic sequence is given by:

Substitute the values:
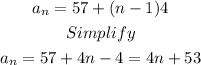
Answer:
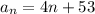
c) For n = 9, we have:
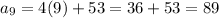
Answer: he scores 89 in the 9th quiz.