Question

Find an nth-degree polynomial function with real coefficients satisfying the given conditions. If you are using a graphing utility, use it to graph the function and verify the real zeros and the given function valuen=34 and 5i are zerosf(1)= -78f(x)=

Answer 1

f(x) = x³ - 4x² + 25x - 100

Step-by-step explanation

The degree of the polynomial is 3, so there are 3 factors,

`f(x)=(x-x_1)(x-x_2)(x-x_3)_{}`

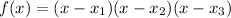
Two of the zeros are 4 and 5i. The second given zero is complex, so its complex conjugate must be a zero too. Therefore, the third zero is -5i,

`f(x)=(x-4)(x-5i)(x+5i)`

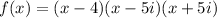
Let's verify that f(1) is -78,

`f(1)=(1-4)(1-5i)(1+5i)`

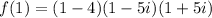
The product of a complex number and its complex conjugate is the sum of the squares of the real and imaginary parts because it has the form of a difference of two squares,

`\begin{gathered} f(1)=(-3)(1^2-(5i)^2) \\ f(1)=(-3)(1-(-25)) \\ f(1)=(-3)(1+25) \end{gathered}`

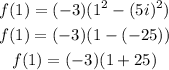
Solve the product,

`f(1)=-3\cdot26=-78`

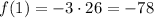
Thus, the zero we found is correct. Now we have to write the function in standard form, by multiplying the factors,

`\begin{gathered} f(x)=(x-4)(x-5i)(x+5i)=f(x)=(x-4)(x^2-5ix+5ix-5i\cdot5i) \\ f(x)=(x-4)(x^2+25) \end{gathered}`

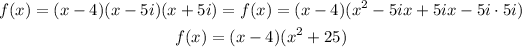
Multiply these two factors,

`f(x)=x^3-4x^2+25x-100`

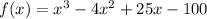
Hence, the function that satisfies the given conditions is f(x) = x³ - 4x² + 25x - 100