Answer:
2^-3
Step-by-step explanation:
To write the equivalent expression, we first realize that 4 = 2^2; therefore, the expression can be written as
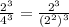
With can further be rewritten as
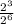
Next, we use the property of the exponents that
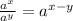
to write the above as
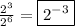
which is our answer!