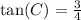GivenHiven the Right Triangle ABC, you can find the missing side AB using the Pythagorean Theorem. This states that:
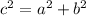
Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.
In this case:
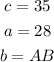
Then, substituting values and solving for AB, you get:
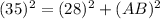
![\begin{gathered} \sqrt[]{(35)^2-(28)^2}=AB \\ \\ \sqrt[]{441}=AB \\ \\ AB=21 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c5l0gaevly7pfkeojcaqcklrayruleqbf2.png)
By definition:
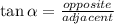
In this case, you can identify that:
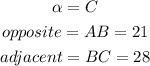
Therefore:
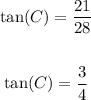
Hence, the answer is: