It is given that the diameter of the base of the cone is AB=20, and the slant height is BC=10.
Recall that the radius is one-half of the diameter, it follows that:
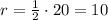
Note that the radius (r), vertical height (h), and slant height (l) of a cone form a right triangle which satisfies the Pythagorean Theorem:
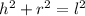
Substitute r=10 and l=10 into the equation:
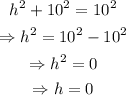
Notice that the height of the cone is calculated to be zero which is not possible for a cone.
The Surface Area of a cone is:
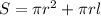
Substitute r=10 and l=10 into the formula:
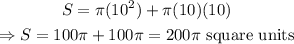
The answer is 200π square units.