Ok, so
Let me draw the situation here below:
Remember that the slope of a line is given by the formula:
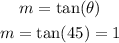
The slope of our line will be 1.
Now, we could use the equation:
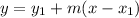
Where (x1,y1) is a point of the line and m is the slope. Replacing our values:
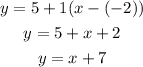
Therefore, the equation is y=x+7.