Question

A “blink of an eye” is a time interval of about 150 ms for an average adult. The “closure” portion of the blink takes only about 55 ms. Let us model the closure of the upper eyelid as uniform angular acceleration through an angular displacement of 17.1°.What is the value of the angular acceleration the eyelid undergoes while closing? What is the tangential acceleration of the edge of the eyelid while closing if the radius of the eyeball is 1.25 cm?

Answer 1

The angular acceleration is 197.02 rad/s^2

The tangential acceleration is 2.46 m/s^2

Explanation:

We must consider the blinking of the eyes as a constant circular movement. The initial angular velocity of the closing portion of the eye is taken to be zero assuming it starts from rest. The general formula for the rotational kinematics equation can be applied to find the constant angular acceleration.

The first thing is to convert the time interval of the closing portion of the blink from ms to s.

`t=55\text{ ms}\cdot\frac{1\text{ s}}{1000\text{ ms}}=0.055\text{ s}`

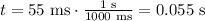
Now, we convert the angular displacement of the eyelid from degrees to rad:

`\begin{gathered} \theta=17.1\text{\degree}\cdot\frac{2\pi\text{ rad}}{360\text{\degree}}= \\ \theta=0.298\text{ rad} \end{gathered}`

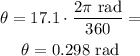
Let α be the constant angular acceleration experienced by the eyelid as it closes and consider the eyelid to start from rest. We calculate the angular acceleration of the eyelid as it closes.

`\begin{gathered} \Delta\theta=\omega_1+(1)/(2)\alpha(t)^2 \\ \omega_1=0 \\ \text{ therefore:} \\ \Delta\theta=(1)/(2)\alpha(t)^2 \\ \text{ Solving for }\alpha \\ \alpha=(2\cdot\Delta\theta)/(t^2) \\ \text{ Replacing:} \\ \alpha=(2\cdot0.298)/((0.055)^2) \\ \alpha=197.02rad/s^2 \end{gathered}`

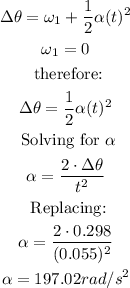
Therefore, the magnitude of the angular acceleration is 197.02 rad/s^2

Tangential acceleration is the acceleration produced by the eyelid tangential to the direction of its movement. It is numerically equal to the radius times the angular acceleration of the eyelid.

We need to convert the radius of the eyeball from cm to m.

`r=1.25\text{ cm}\cdot\frac{1\text{ m}}{100\text{ cm}}=0.0125\text{ m}`

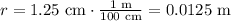
We calculate the tangential acceleration:

`\begin{gathered} \alpha_1=r\cdot\alpha \\ \text{ Replacing} \\ \alpha_1=0.0125\cdot197.02 \\ \alpha_1=2.46m/s^2 \end{gathered}`

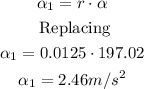
Therefore, the tangential acceleration of the eyeball is 2.46 m/s^2