Question

I would like help with #2 I forget how to find local and absolute Extrema values thanks!

Answer 1

The first step to find the extrema values of a function is to find its derivative:

`\begin{gathered} f(x)=x^2e^(-x) \\ f^(\prime)(x)=2xe^(-x)-x^2e^(-x) \end{gathered}`

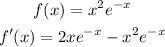
We know that the extrema values (local or absolute maximum or minimum) occur at points in which the derivative of the function has a value of zero. To find these points we have to make the derivative equal to 0 and solve the expression for x, this way:

`\begin{gathered} 0=2xe^(-x)-x^2e^(-x) \\ 0=e^(-x)(2x-x^2) \end{gathered}`

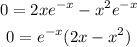
There is no possible way for e^-x to be 0, which means that 2x-x^2 must be 0:

`\begin{gathered} 0=2x-x^2 \\ 0=x(2-x) \\ 0=2-x \\ x=2 \\ x=0 \end{gathered}`

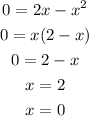
It means that there is an extrema value at x=0 and at x=2.

To find their values we just have to evaluate the function at these points, it means we have to find f(0) and f(2):

`\begin{gathered} f(0)=0^2e^(-0)=0 \\ f(2)=2^2e^2=4e^2=29.6 \end{gathered}`

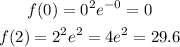
The local or absolute extrema values in the given interval are 0 and 29.6.